Sliding on the Earth's surface

Sliding on sphere

Falling off the edge of the Earth? so if the Earth is sphere why don’t we fall off the edge? The answer, as you already know it, is because of gravity. This means, because gravity is pulling you down you are unable to leave off the ground, as the saying goes what goes up must come down. The key word here is down, which –in this case– refers to the center of the Earth and this is true wherever you are in our planet. And it is precisely because of this that satellites are able to orbit our planet. Orbiting Earth is, of course, a diplomatic way of saying that the satellites keep falling to the center of the Earth but kept missing the surface of Earth. Hypothetically let us assume that a person is given a horizontal velocity from the top of the Earth as shown in Fig. 1. What must be the minimum initial speed if the person is never to hit the Earth’s surface after it is set in motion?

This is a two dimensional motion, meaning the person is going to fall along the vertical axis while also traveling horizontally. Think of the path followed as half-parabola (inverted parabola). It is worth mentioning that he time takes the person to travel the height along the y-axis and the time it takes to cover the distance in the x-axis is the same. Using two-dimensional equations of motion we can precisely determine the path the person will follow. The height measured from the bottom of the Earth, i.e south pole in Fig. 1, is the diameters \(D=2R\), and assume the horizontal distance is \(R_x\). The trajectory in the y-axis as described by one of (uniformly accelerated rectilinear motion) UARM equations is \(R_y=D-0.5\mathrm{gt}^2\), which with \(t=R_x/v_0\) yields

\[\begin{aligned} R_y=D-\frac{\mathrm{g}R_x^2}{2\mathrm{v}_0^2} \label{eq:one1}. \end{aligned}\]

At a point where the height is \(R_r\) the points on the Earth’s surface are described as \(R_r^2+R_x^2=D^2\). Notice that when \(R_x=0\), implying \(t=0\), it follows that \(R_r=R_y\). Other than that for the rest of the points \(R_x\) we demand the person to be above the Earth’s surface which mathematically is put as: \(R_y > R_r\), indicating \(R_y^2+R_x^2>D^2\)

\[\begin{aligned} \Big(D-\frac{\mathrm{g}R_x^2}{2\mathrm{v}_0^2}\Big)^2+R_x^2 > D^2\\ R_x^2+\frac{\mathrm{g^2}R_x^4}{4\mathrm{v}_0^4} > \frac{\mathrm{g}R_x^2 D}{\mathrm{v}_0^2} \label{eq:one2}. \end{aligned}\]

Notice here that if the equality holds fo \(R_x\rightarrow0\), it means it is true for all values of \(R_x\). If the person’s trajectory has large enough radius of curvature at the beginning, the person won’t touch the Earth’s surface for \(v_0 > \sqrt{\mathrm{g}D}\). With this speed the person can free herself from being bounded to Earth due to gravity .

Noting that \(D=2R\) the initial speed takes the form \(v_0 = \sqrt{2\mathrm{g}R}\). Looking at this result closely might ring a bell, i.e. escape velocity. Then one can readily show that:\(v_0 = \sqrt{2\mathrm{g}R}=\sqrt{2\frac{GM}{R^2}R}=v_{esc}\).

Recall that \(\mathrm{g}=\frac{GM}{R^2}\), also note here that \(v_0 = \sqrt{\mathrm{g}R}\) is the orbital speed, which is a factor \((\sqrt{2})^{-1}\) less than the escape velocity.

But instead of given an initial speed to start the motion, what if we imagined that the person is sliding on the surface of the Earth? what will the physics inform us about this kind of situation? Can the person be able to complete a circle, return to where it started, around the sphere? if not until which point can she slide before ’falling off’? Will it be fun? I would presume this would be like traveling in a straight line, because the curvature is long it is hard to notice. This sliding on a sphere is actually a very common question that one finds on physics textbooks. I will like to extend, to an exaggerated extent, on to sliding on the Earth’s surface. The usual question answers the height, or the angle, at which the object losses contact with the sphere. It loses contact when it falls off of the sphere. Now let us replace the person by an object as it doesn’t make any difference on the discussion. Imagine then the object is sliding on the surface of the Earth and revisit the textbook problem again.

To make our discussion comprehensive we consider here two situations: the first case is where we consider an unrealistic situation and assume the surface of the Earth to be frictionless. In fact this could demand a situation where every part of the Earth is covered with ice. Surprisingly this is not far fetched phenomenon to imagine as Earth’s surface became completely or nearly completely frozen once. This according to Snowball Earth hypothesis happened during the Cryogenian –period before 650 million years ago. The second case is somewhat closer to the reality at present, in this situation we consider the effect of friction.

Sliding on a Snowball Earth

The most commonly occurring textbook question is the case of frictionless situation, in this scenario the object starts from top of the sphere and slides down the surface. We want to know at what height, or what should be the minimum angle, at which the object leaves the surface. For the case at hand we assume that the coefficient of friction between the snowball Earth and the object is zero. Although in reality it is small but non zero. We show in Fig. 3 the schematic representation of free body of the object, we assume it slides from the top of the sphere, the diagram shows the forces acting on the sliding object after it slides and reaches point C

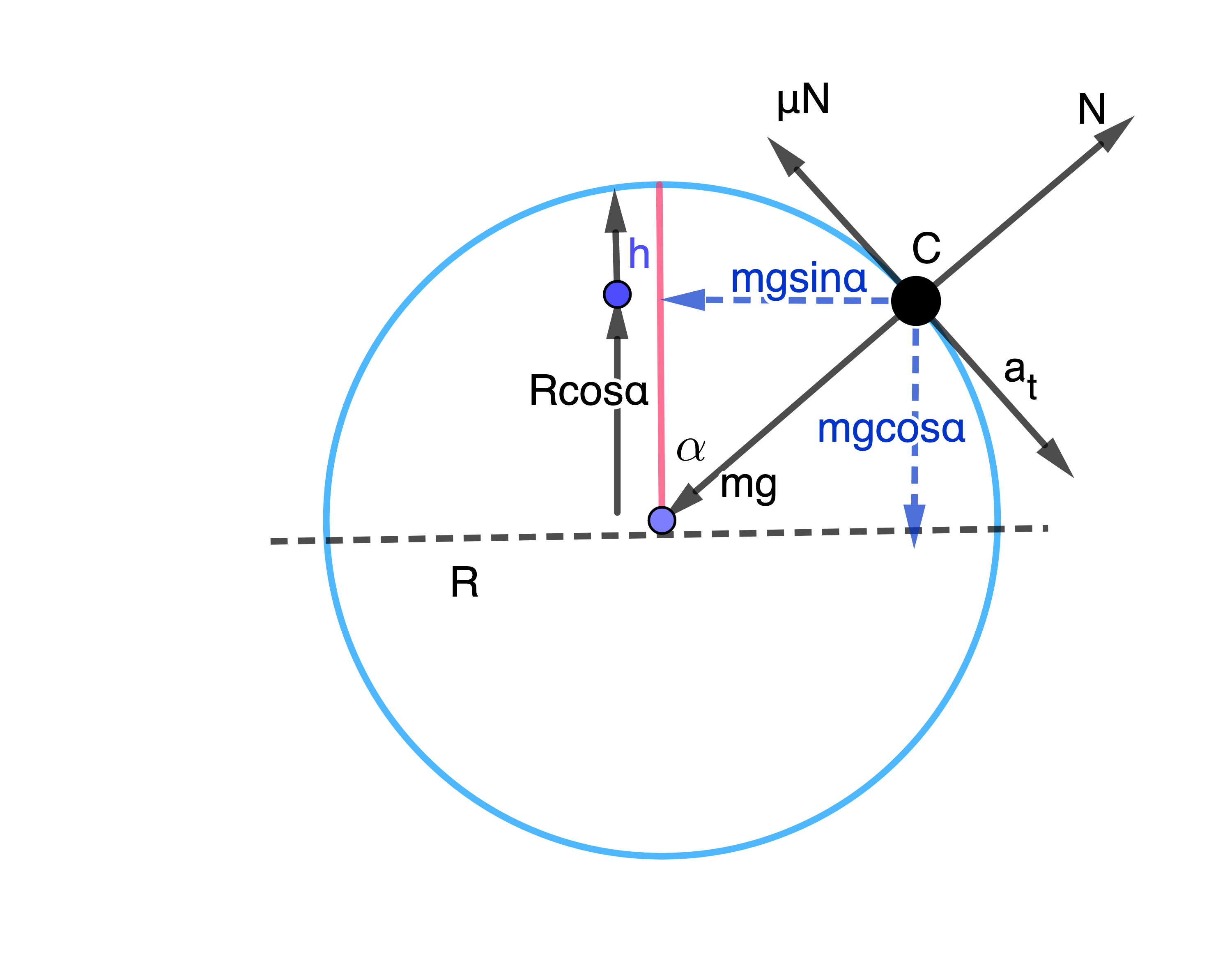
We use Newton’s second law which is mathematically expressed as \(\vec F_{\mathrm{ext}} = \mathrm{m}\vec a\). In our case we will take the vector sum of all the external forces acting on the object. We schematically draw the free-body diagram of these forces acting on the sliding object in Fig. 3. It is seen that the centripetal force \(\frac{\mathrm{m}v^2}{R}\), that is pulling the system inward, is balanced by force components of \(\mathrm{mg}\cos\alpha - \mathrm{N}\). At the point of loss of contact we set the normal force \(\mathrm{N}=0\); and recalling centripetal force is given by \(\frac{mv^2}{R^2}\)

\[\begin{aligned} \mathrm{mg}\cos\alpha &= \frac{\mathrm{m}v^2}{R}\\ v^2 &= gR\cos\alpha ..............................(1) \label{eq:one}. \end{aligned}\]

Interestingly this result is independent of the mass of the object. This implies that the result is valid in all planets including the moon provided that \(g, R\) are redefined to take the values of the planet in consideration. On the other hand from energy conservation consideration we note that, in a simplistic view, the kinetic energy at the north-pole is converted into potential energy at height \(h\) (measured from the top). This same height, measured from the center of the circle, can be recasted into \(R(1-\cos\alpha)\). We can cross-check ourselves by making sanity check and that is the sum of these two heights should equal the radius of the Earth.

\[\begin{aligned} \frac{1}{2} \mathrm{m}v^2 &= \mathrm{mg}R(1-\cos\alpha), \\ v^2 &=2\mathrm{g}R(1- \cos\alpha)\\ \cos\alpha &= \frac{2}{3}. ..............................(2) \label{eq:two}. \end{aligned}\]

From which it follows that the height at which the object leaves is \(R(1-\cos\alpha)=\frac{R}{3}\), the corresponding angle is \(\cos^{-1}(2/3)\approx 48.2^0\). Once again the interesting aspect of Eq. (2) is that it is independent of mass and acceleration due to gravity, this implies that the result is the same in any planet.

Sliding on Earth’s surface: case with friction

The above discussion is not only simplified but also unrealistic. Although realistic simulation of the situation requires the involvement of several parameters including but not limited to wind, pressure, temperature, air resistance etc. For the sake of simplicity and close to realistic implementation let us include the effect of friction only. This means that now we are assuming the sphere to be no more frictionless; in this case also we will apply Newton’s second law as in previous section (with non-zero Normal force). Moreover we now apply the second law again to the tangential component too

\[\begin{aligned} \mathrm{mg}\cos\alpha - \mathrm{N} &= \frac{\mathrm{m}v^2}{R}\\ \mathrm{N} &= \mathrm{mg}\cos\alpha -\frac{\mathrm{m}v^2}{R}. .............................(3)\\ \label{eq:three}. \end{aligned}\]

In a similar manner, from the tangential component, we get

\[\begin{aligned} \mathrm{mg}\sin\alpha - \mu\mathrm{N} &=\mathrm{m}a_t\\ \frac{dv}{dt} &= \mathrm{g}(\sin\alpha-\mu\cos\alpha)+\mu\frac{v^2}{R}. .............................(4) \label{eq:four}. \end{aligned}\]

With the introduction of the following chain rule

\[\begin{aligned} \frac{dv}{dt} &= \frac{dv}{d\alpha} \frac{d\alpha}{dt} \\ 2v\frac{dv}{d\alpha} &= \frac{d(v^2)}{d\alpha} ..............................(5) \label{eq:five}. \end{aligned}\]

At this juncture it is worth introducing dimensional analysis. Dimensional analysis is the process of converting between units. This is a problem-solving strategy that uses the fact that any number or expression can be multiplied by one without changing its value. We can rewrite Eq. (5) as

\[\begin{aligned} \mathrm{g}(\sin\alpha-\mu\cos\alpha)+\mu\frac{v^2}{R} &= \frac{1}{2R} \frac{d(v^2)}{d\alpha} \\ \frac{d(V^2)}{d\alpha} -2\mu V^2 &= 2(\sin\alpha-\mu\cos\alpha). ..............................(6) \label{eq:six}. \end{aligned}\]

where \(V\equiv\frac{v}{\sqrt{\mathrm{g}R}}\) is dimensionless quantity. In dimensional analysis, a dimensionless quantity is a quantity without any physical units, this means it is just a pure number. Because when doing dimensionless analysis we are either taking a product or ratio of quantities with physical units, what comes out is a number without units. For our case, as an example we see below:

\[\begin{aligned} \mathrm{[V}] &=\frac{[v]}{\sqrt{[\mathrm{g]}[R]}}\\ &=\mathrm{\frac{[LT^{-1}]}{\sqrt{[\mathrm{LT^{-2}]}[L]}}} =\mathrm{\frac{[LT^{-1}]}{[LT^{-1}]}} \label{eq:sixb}. \end{aligned}\]

The introduction of this dimensionless parameter facilitates the scale-up of obtained results to general case. This help us assess the relative importance of parameters in our equation. Such analysis also help us identify the key parameters in controlling the physical system.

Solution of Eq. (6), provided below, informs us that the object will come to rest, cause of friction, before it reaches the equator. At the equator the angle \(\pi/2\) , and for this to happen the coefficient of friction should be infinity. With that much of friction obviously the object won’t move. But the general expression is \(\pi/2-1.5/\mu\).

Brief glimpse at the solution

We follow the footsteps outlined in this paper. We won’t go in details but briefly outline the steps. To begin with equations like Eq. (6) can be solved, say using trial form \(V_1^2 = A\cos\alpha + B\sin\alpha\). Let us plug in this form into Eq. (6) and then separately equate sine and cosine terms to obtain

\[\begin{aligned} V_1^2 &= \frac{(4\mu^2-2)\cos\alpha-6\mu\sin\alpha}{1+4\mu^2}. ..............................(7) \label{eq:seven}. \end{aligned}\]

On the other hand setting right hand side of Eq. (6) to zero yields the solution of the form

\[\begin{aligned} \frac{d(V^2)}{(V^2)} &= 2\mu \mathrm{d}\alpha\\ V^2 &= Ce^{2\mu\alpha}. ..............................(8) \label{eq:eight}. \end{aligned}\]

To windup, now let us combine the solutions, noting \(V_1^2+V_2^2\) is also the solution, combining all this the final solution takes the form

\[\begin{aligned} V^2 &= \frac{(2-4\mu^2)(e^{2\mu\alpha}-\cos\alpha)-6\mu\sin\alpha}{1+4\mu^2}+V_0^2e^{2\mu\alpha} ..............................(9) \label{eq:nine}. \end{aligned}\]

setting \(V=0\) for \(\alpha=\pi/2\) Eq. (9) solved for \(V_0\) yields.

\[\begin{aligned} V_0^2 &= \frac{(4\mu^2-2)\sin\delta+6\mu(e^{-\mu\delta}-\cos\delta)}{1+4\mu^2}. ..............................(10) \label{eq:ten}. \end{aligned}\]

At \(\delta=0\) the result is zero. Also it equals \((3\mu\delta-2)\delta\) when expanding to second order in \(\delta\). Hence \(V^2\) is negative when \(\delta\) is infinitesimally small. This means the particle cannot reach the equator. It must stop at some smaller angle. How close can it come to equator? To get the result we maximize the angle using \(\frac{d\alpha}{d(V^2)}\rightarrow0\) at \(V=0\).

Consequently \(\mu\rightarrow\infty\), thus

\[\begin{aligned} V_0^2 &= \sin\delta-\frac{3}{2\mu}\cos\delta. ..............................(11) \label{eq:eleven}. \end{aligned}\]

Meaning the object comes to rest at or near \(\pi/2-1.5/\mu\)